文章同步链接芒果浩明

排序算法小结

1、冒泡排序

冒泡排序（Bubble Sort）是一种比较简单的排序，思路是通过重复走访需要排序的序列，而后比较相邻的两个元素，假如前者大于后者，那么交换两元素。继续走访交换下去，那么最后的一个元素就是最大的元素了。

Bubble_sort_animation.gif

算法

1. 比较相邻的两个元素，假如前者大于后者，那么交换两个元素。
2. 对每一对元素执行相同的操作，从开始的第一对到序列最后一对。这步完成后，序列最后一个元素就是最大元素。
3. 除去最后一个元素，对序列执行1、2步操作。直到序列范围缩小到没有数字需要比较。

这是升序排序流程，降序修改比较条件就可，即把最小的元素交换到最后序的位置。

代码实现

//c++void bubbleSort(vector<int> &arr)    {        if (arr.empty())    return;        size_t length = arr.size();        for (size_t i = 0; i < length - 1; ++i)//i每添加1,得到一个最大值元素            for (size_t j = 0; j < length - 1 - i; ++j)// -i除去最后一个最大元素                if (arr[j] > arr[j + 1])//交换条件                    swap(arr[j], arr[j + 1]);    }

算法复杂度

• 时间复杂度
  对于n个元素需要比较n*n次，时间复杂度为O(n^2)
• 空间复杂度
  额外的内存开销只有一个交换次序使用的临时变量，所以空间复杂度为O(n)

2、选择排序

选择排序（Selection Sort)也比较简单直观。以升序为例，选择排序工作原理为，从为排序的元素之中筛选出最小的元素放入序列初始位置。继续筛选最小的元素，放入排序的序列末尾。直到筛选完所有元素。

Selection_sort_animation.gif

代码实现

//c++//选择排序    void selectionSort(vector<int> &arr)    {        if (arr.empty())    return;        int length = arr.size();        int min_index = 0;//记录最小元素的位置        for (int i = 0; i < length - 1; ++i)        {            min_index = i;//排好顺序的末尾作为最小元素            for (int j = i + 1; j < length; ++j)                if (arr[min_index] > arr[j])                    min_index = j;            //找到最小元素，交换放到已排序末尾            std::swap(arr[min_index], arr[i]);        }    }

算法复杂度

• 时间复杂度
  选择排序需要比较的次数和冒泡排序是一样的，所以时间复杂度为O(n^2)。选择排序相比冒泡排序的优点是，减少了交换的次数。冒泡排序可能每次比较之后都需要交换，选择排序则是比较完所有未排序的元素才进行交换。
• 空间复杂度
  空间复杂度和冒泡一样都是O(n),需要辅助空间O(1)。

3、 插入排序

插入排序（Insertion Sort）算法也是比较直观的。原理是前半部分为已经排序，紧接着未排序的一个元素取出来，向前扫描比较，找到合适的位置插入。为了完成插入操作，就需要把已经排序的元素逐渐向后挪位。整个过程笔者觉得和我们平常打麻将时整牌的过程有点像。

Insertion_sort_animation.gif

代码实现

//c++//插入排序    void insertionSort(vector<int> &arr)    {        if (arr.empty()) return;        int lenght = arr.size();        for (int i = 1; i < lenght; ++i)        {            int key = arr[i];//取出未排序的元素            int j = 0;            for ( j = i - 1; j >= 0 && arr[j] > key; --j)//往前扫描                arr[j + 1] = arr[j];//同时元素往后挪位            arr[j + 1] = key;//合适位置插入        }    }

算法复杂度

• 时间复杂度
  与冒泡和选择一样，for循环嵌套for循环。扫描遍历时比较的次数是O(n^2)。和选择排序一样，插入排序相比冒泡排序交换次数更少。
• 空间复杂度
  需要辅助空间O(1),空间复杂度依然是O(n^2)

4、 希尔排序

希尔排序（Shell Sort）,也称为递减增量排序算法。是插入排序]的一种更高效的改进版本。希尔排序是非稳固排序算法 。是第一个突破O(n^2)的排序算法。算法的主要思想是把一个序列划分位几个区域来提升插入排序的性能，一轮插入排序完成，缩小划分区域，继续插入排序。划分的方式是引入一个步长的概念。

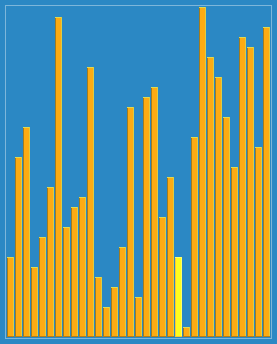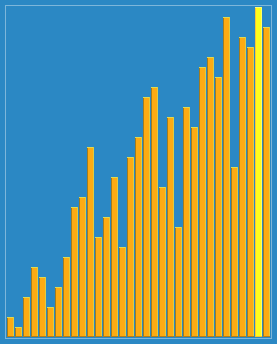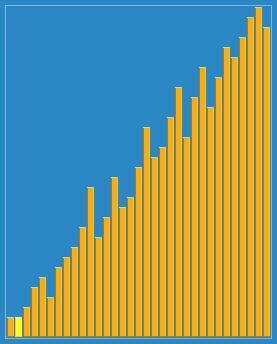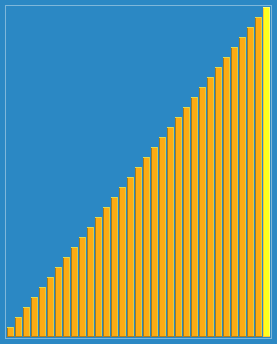Sorting_shellsort_anim.gif

例如

需要排序的数组为[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]

以步长为5划分，进行排序。

//step_size = 513 14 94 33 8225 59 94 65 2345 27 73 25 3910

而后，对每一列进行排序。注意是，每一列，每一列才表现了步长的概念。

10 14 73 25 2313 27 94 33 3925 59 94 65 8245

而后复原到一维数组观察，[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了，而后再以3为步长进行排序：

//step_size = 310 14 7325 23 1327 94 3339 25 5994 65 8245

同样的对每一列排序，得到

10 14 1325 23 3327 25 5939 65 7345 94 8294

在复原为一维数组，最后步长设置为1。就是简单的插入排序。

从上面可以看出，排序的过程与递减增量排序的名字是相吻合的。通过递减的步长划分区域，排序，最后步长为1的时候就是普通的插入排序。前面的步长递减的工作就是给最后步长为1的普通插入排序做优化的。

代码实现

//c++//希尔排序    void shellSort(vector<int> &arr)    {        if (arr.empty())    return;        int lenght = arr.size();        //动态步长        int step_size = 0;        while (step_size < lenght / 3)            step_size = step_size * 3 + 1;        while (step_size >= 1)        {            //step_size = 1,就是普通的插入排序            for (int i = step_size; i < lenght; ++i)            {                int key = arr[i];//取出未插入的值                int j;                for (j = i - step_size; j >= 0 && key < arr[j]; j -= step_size)//元素往后挪位                    arr[j + step_size] = arr[j];//同时元素往后挪位                arr[j + step_size] = key;//合适位置插入            }            step_size /= 3;        }    }

算法复杂度

• 时间复杂度
  时间复杂度会随着步长的变换而变化。

• 空间复杂度

  内存开销和普通插入排序一样，空间复杂度都是O(n)

5、 快速排序

快速排序（Quick Sort)，又称为划分交换排序。采用的是分治法的思想。

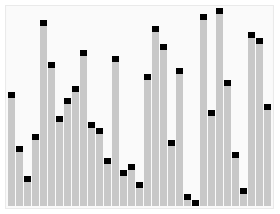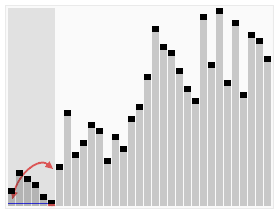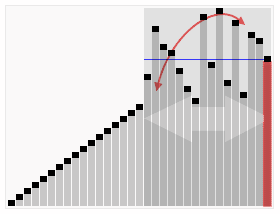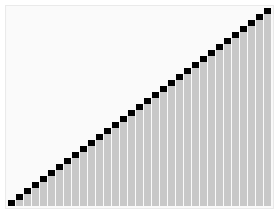Sorting_quicksort_anim.gif

算法步骤为

1. 从数列中挑出一个元素，称为"基准"（pivot），
2. 重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任何一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3. 递归地recursively把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归到最底部时，数列的大小是零或者一，也就是已经排序好了。这个算法肯定会结束，由于在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

代码实现

//1、直接调用库函数sort(a, a + n);//2、快速排序(递归方法）    void quickSort(vector<int> &arr)    {        if (arr.empty()) return;        quickSortHelper(arr, 0, arr.size() - 1);    }    void quickSortHelper(vector<int> &arr, int low, int high)    {        int l = low;        int h = high;        int pivot = arr.at(low);//选取基准        while (low < high)        {            while (low < high && pivot < arr.at(high))                --high;            if (low < high)                arr.at(low++) = arr.at(high);            while (low < high && pivot > arr.at(low))                ++low;            if (low < high)                arr.at(high++) = arr.at(low);        }        arr.at(low) = pivot;//基准放到正确位置                            //此时low == high        if (l < low - 1)            quickSortHelper(arr, l, low - 1);        if (h > high + 1)            quickSortHelper(arr, high + 1, h);    }//3、快速排序（迭代方法）struct Range{    int start, end;    Range(int s = 0, int e = 0)    {        start = s;        end = e;    }};void quickSort(vector<int> &arr){    if (arr.empty()) return;    int len = arr.size();    stack<Range> r;    r.push(Range(0, len - 1));//第一个范围入栈    while (!r.empty())    {        Range tmp = r.top();//取出压入的栈，相当于递归调用        r.pop();        if (tmp.start >= tmp.end)            continue;//迭代截至条件        int mid = arr[tmp.end];//去最后一个元素作为基准        int left = tmp.start, right = tmp.end - 1;//在此范围内遍历与基准作比较        while (left < right)        {            //把元素以基准划分为两部分            while (arr[left] < mid && left < right) ++left;            while (arr[right] > mid && left < right) --right;            std::swap(arr[left], arr[right]);        }        if (arr[left] >= arr[tmp.end])            std::swap(arr[left], arr[tmp.end]);        else            ++left;        r.push(Range(tmp.start, left - 1));//左边压栈下去        r.push(Range(left + 1, tmp.end));//右边压栈下去    }}

6、 归并排序

归并排序（Merge sort，或者mergesort），是创立在归并操作上的一种有效的排序算法，效率为[图片上传失败...(image-314c2b-1535378924674)]

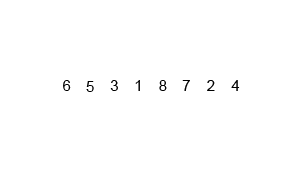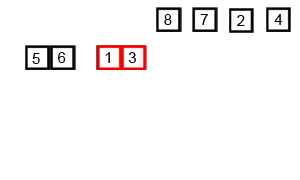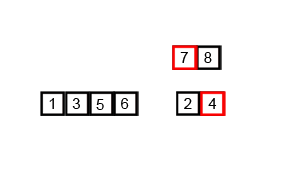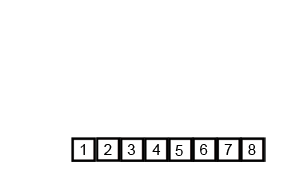Merge-sort-example-300px.gif

代码实现

//归并排序    void mergeSort(vector<int> &arr)    {        if (arr.empty()) return;        mergeSortHelper(arr, 0, arr.size() - 1);    }    void mergeSortHelper(vector<int> &arr, int first, int last)    {        int mid = 0;        if(first < last)        {            mid = first + (last - first) / 2;            mergeSortHelper(arr, first, mid);            mergeSortHelper(arr, mid + 1, last);            merge(arr, first, mid, last);        }    }    //合并有序数组arr[first....mid] 和 arr[mid+1 ...last] 到arr[first...last]中    void merge(vector<int> &arr, int first, int mid, int last)    {        vector<int> tmp(arr.begin(), arr.end());        int le = first;        int ri = mid + 1;        int tm = 0;        while (le <= mid && ri <= last)        {            if (arr[le] < arr[ri])                tmp[tm++] = arr[le++];            else                tmp[tm++] = arr[ri++];        }        while (le <= mid)            tmp[tm++] = arr[le++];        while (ri <= last)            tmp[tm++] = arr[ri++];        arr = tmp;    }

7、 堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或者索引总是小于（或者者大于）它的父节点。

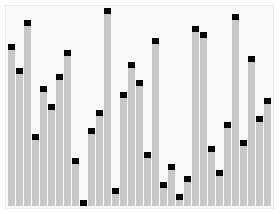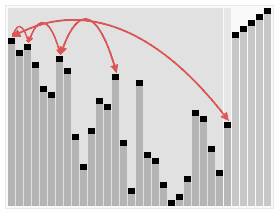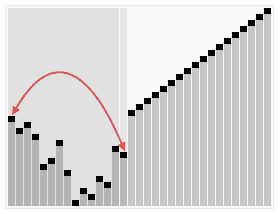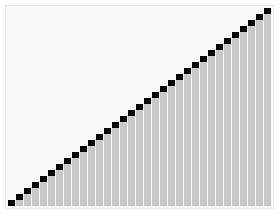Sorting_heapsort_anim.gif

代码实现

//堆排序    //利用最大堆初始化调整可以得到递增序列    void maxHeap(vector<int> &arr, int start, int end)    {        int dad = start;        int son = dad * 2 + 1;                while (son <= end)        {            if (son + 1 <= end && arr[son] < arr[son + 1])                ++son;//选择最大的子节点            if (arr[dad] > arr[son])                return; //调整结束            else            {                //否则进行调整                swap(arr[dad], arr[son]);                //继续向下调整                dad = son;                son = 2 * son + 1;            }        }    }    //利用最小堆可以得到递减序列    void minHeap(vector<int> &arr, int start, int end)    {        int dad = start;        int son = 2 * dad + 1;        while (son <= end)        {            if (son + 1 <= end && arr[son] > arr[son + 1])                ++son;//找最小的子节点            if (arr[dad] < arr[son])                return;            else            {                swap(arr[dad], arr[son]);                dad = son;                son = dad * 2 + 1;            }        }    }    void heapSort(vector<int> &arr)    {        if (arr.empty()) return;        int len = arr.size();        //先初始化为一个最大堆，从最后一个父节点开始调整        for (int i = len / 2 - 1; i >= 0; --i)            maxHeap(arr, i, len - 1);        //进行堆的删除操作，再重新调整        for (int i = len - 1; i >= 1; --i)        {            swap(arr[i], arr[0]);//每次的arr[0]都是最大值，所以得到递增序列            maxHeap(arr, 0, i - 1);        }    }

完整代码

#include "stdafx.h"#include<iostream>#include<vector>#include<stack>using namespace std;class MySort{public:    //冒泡排序    void bubbleSort(vector<int> &arr)    {        if (arr.empty())    return;        size_t length = arr.size();        for (size_t i = 0; i < length - 1; ++i)//i每添加1,得到一个最大值元素            for (size_t j = 0; j < length - 1 - i; ++j)// -i除去最后一个最大元素                if (arr[j] > arr[j + 1])//交换条件                    swap(arr[j], arr[j + 1]);    }    //选择排序    void selectionSort(vector<int> &arr)    {        if (arr.empty())    return;        int length = arr.size();        int min_index = 0;//记录最小元素的位置        for (int i = 0; i < length - 1; ++i)        {            min_index = i;//排好顺序的末尾作为最小元素            for (int j = i + 1; j < length; ++j)                if (arr[min_index] > arr[j])                    min_index = j;            //找到最小元素，交换放到已排序末尾            std::swap(arr[min_index], arr[i]);        }    }    //插入排序    void insertionSort(vector<int> &arr)    {        if (arr.empty()) return;        int lenght = arr.size();        for (int i = 1; i < lenght; ++i)        {            int key = arr[i];//取出未排序的元素            int j = 0;            for ( j = i - 1; j >= 0 && arr[j] > key; --j)//往前扫描                arr[j + 1] = arr[j];//同时元素往后挪位            arr[j + 1] = key;//合适位置插入        }    }    //希尔排序    void shellSort(vector<int> &arr)    {        if (arr.empty())    return;        int lenght = arr.size();        //动态步长        int step_size = 0;        while (step_size < lenght / 3)            step_size = step_size * 3 + 1;        while (step_size >= 1)        {            //step_size = 1,就是普通的插入排序            for (int i = step_size; i < lenght; ++i)            {                int key = arr[i];//取出未插入的值                int j;                for (j = i - step_size; j >= 0 && key < arr[j]; j -= step_size)//元素往后挪位                    arr[j + step_size] = arr[j];//同时元素往后挪位                arr[j + step_size] = key;//合适位置插入            }            step_size /= 3;        }    }    //快速排序(递归方法）    void quickSort(vector<int> &arr)    {        if (arr.empty()) return;        quickSortHelper(arr, 0, arr.size() - 1);    }    void quickSortHelper(vector<int> &arr, int low, int high)    {        int l = low;        int h = high;        int pivot = arr.at(low);//选取基准        while (low < high)        {            while (low < high && pivot < arr.at(high))                --high;            if (low < high)                arr.at(low++) = arr.at(high);            while (low < high && pivot > arr.at(low))                ++low;            if (low < high)                arr.at(high++) = arr.at(low);        }        arr.at(low) = pivot;//基准放到正确位置                            //此时low == high        if (l < low - 1)            quickSortHelper(arr, l, low - 1);        if (h > high + 1)            quickSortHelper(arr, high + 1, h);    }    //归并排序    void mergeSort(vector<int> &arr)    {        if (arr.empty()) return;        mergeSortHelper(arr, 0, arr.size() - 1);    }    void mergeSortHelper(vector<int> &arr, int first, int last)    {        int mid = 0;        if (first < last)        {            mid = first + (last - first) / 2;            mergeSortHelper(arr, first, mid);            mergeSortHelper(arr, mid + 1, last);            merge(arr, first, mid, last);        }    }    //合并有序数组arr[first....mid] 和 arr[mid+1 ...last] 到arr[first...last]中    void merge(vector<int> &arr, int first, int mid, int last)    {        vector<int> tmp(arr.begin(), arr.end());        int le = first;        int ri = mid + 1;        int tm = 0;        while (le <= mid && ri <= last)        {            if (arr[le] < arr[ri])                tmp[tm++] = arr[le++];            else                tmp[tm++] = arr[ri++];        }        while (le <= mid)            tmp[tm++] = arr[le++];        while (ri <= last)            tmp[tm++] = arr[ri++];        arr = tmp;    }    //堆排序    //利用最大堆初始化调整可以得到递增序列    void maxHeap(vector<int> &arr, int start, int end)    {        int dad = start;        int son = dad * 2 + 1;        while (son <= end)        {            if (son + 1 <= end && arr[son] < arr[son + 1])                ++son;//选择最大的子节点            if (arr[dad] > arr[son])                return; //调整结束            else            {                //否则进行调整                swap(arr[dad], arr[son]);                //继续向下调整                dad = son;                son = 2 * son + 1;            }        }    }    //利用最小堆可以得到递减序列    void minHeap(vector<int> &arr, int start, int end)    {        int dad = start;        int son = 2 * dad + 1;        while (son <= end)        {            if (son + 1 <= end && arr[son] > arr[son + 1])                ++son;//找最小的子节点            if (arr[dad] < arr[son])                return;            else            {                swap(arr[dad], arr[son]);                dad = son;                son = dad * 2 + 1;            }        }    }    void heapSort(vector<int> &arr)    {        if (arr.empty()) return;        int len = arr.size();        //先初始化为一个最大堆，从最后一个父节点开始调整        for (int i = len / 2 - 1; i >= 0; --i)            maxHeap(arr, i, len - 1);        //进行堆的删除操作，再重新调整        for (int i = len - 1; i >= 1; --i)        {            swap(arr[i], arr[0]);//每次的arr[0]都是最大值，所以得到递增序列            maxHeap(arr, 0, i - 1);        }    }};//快速排序（迭代方法）struct Range{    int start, end;    Range(int s = 0, int e = 0)    {        start = s;        end = e;    }};void quickSort(vector<int> &arr){    if (arr.empty()) return;    int len = arr.size();    stack<Range> r;    r.push(Range(0, len - 1));//第一个范围入栈    while (!r.empty())    {        Range tmp = r.top();//取出压入的栈，相当于递归调用        r.pop();        if (tmp.start >= tmp.end)            continue;//迭代截至条件        int mid = arr[tmp.end];//去最后一个元素作为基准        int left = tmp.start, right = tmp.end - 1;//在此范围内遍历与基准作比较        while (left < right)        {            //把元素以基准划分为两部分            while (arr[left] < mid && left < right) ++left;            while (arr[right] > mid && left < right) --right;            std::swap(arr[left], arr[right]);        }        if (arr[left] >= arr[tmp.end])            std::swap(arr[left], arr[tmp.end]);        else            ++left;        r.push(Range(tmp.start, left - 1));//左边压栈下去        r.push(Range(left + 1, tmp.end));//右边压栈下去    }}int main(){    vector<int> a = { 1, 5, 2, 3, 4, 9 };    MySort ms;    quickSort(a);    for (auto &v : a)        cout << v << endl;    return 0;}

selfie.jpg