

在本章中,我们将继续探讨监督机器学习中的另一项主要任务,即回归。
分类总是很好的起点,由于它在逻辑上是直观的。
"这是一张图片。告诉我它里面有什么物体。"
"这是一封电子邮件。告诉我它是垃圾邮件还是垃圾邮件。"
"这是医学测试的少量测量结果。告诉我这个人能否患有某种疾病。"
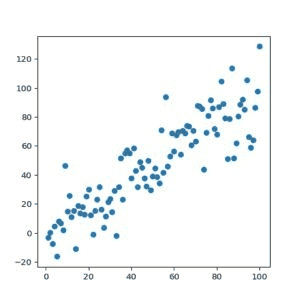
回归也非常直观,且展示方式更直观。比方:
 图片.png
图片.png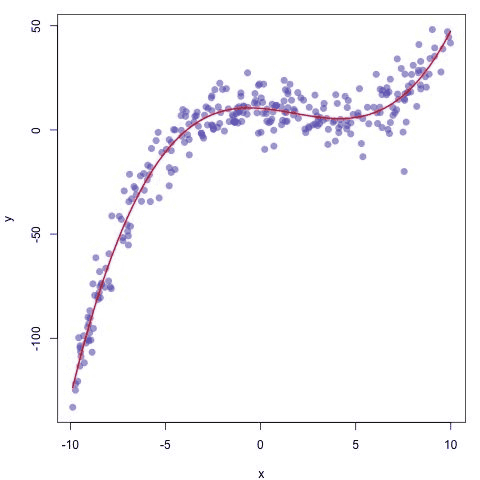 图片.png
图片.png这就是回归的一律。 “这里有少量点,现在告诉我适合这些点的线条或者曲线。”
分类意味着您正在预测某个类别。
回归意味着你在预测数字。这个数字通常是线上的数字。
在回归中,数字实际上的确有意义。
 图片.png
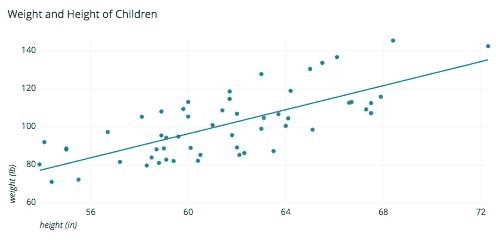
图片.png通过身高体重。或者相反亦然。
当然,身材较高的人体重更大,因而体重更重。这种相关性并不完美,但多数情况的确如此。
例如,您可以想象恐龙的重量远远超过蚂蚁。
房屋的价格可能与居民区的平均家庭收入以及该社区的犯罪率有关。它可能还取决于它的大小,它有多少卧室以及最后一次翻新的属性。当你有多个维度时,你预测的东西不再是一条线。
股票市场的“规则”之一是你应该低买高卖。这样,你总能得到比你投入更多的钱。但很多人有情绪和恐惧。
分析会关注过去10天该股票的价格和新闻等。
X是形状NxD的2D阵列,Y是长度为N的1D阵列.N =样本数,D =输入特征数。
首先,我们实例化模型。假设我们正在使用线性回归。
model = LinearRegression()而后,我们通过调用fit并传入X和Y来训练模型。
model.fit(X, Y)我们还可以通过调用预测函数来进行新的预测。
predictions = model.predict(X)最后,我们可以通过调用score函数来评估模型。
model.score(X, Y)一个细微差别是得分函数不再返回精确度,这只有在我们进行分类时才有意义。由于精确度只是#correct / #total。
当我们有标签时,这是有道理的,由于假如你猜对了标签,那么你是正确的,否则,你不是。但对于回归,这没有意义。精确性可能不是最好的评估指标。通常,衡量回归模型性能的一种方法是使用均方误差(MSE mean squared error)。